Accelerating Molecular Dynamics to Reach Unprecedented Simulation Times with Atomistic Accuracy
Molecular dynamics (MD), the numerical integration of the equations of motions of atoms and molecules, is one of the most powerful tools available to materials scientists, chemists, and biologists, because it provides a fully resolved view of the spatio-temporal evolution of materials. Because of its unparalleled predictive power, MD is extensively used to understand and optimize the properties of current materials, and well as predict the properties of new materials designed in silico. However, MD’s predictive power comes at a considerable computational cost that strongly limits the reach of direct simulations. At first sight, such a computationally intensive problem would appear ideally suited to massively-parallel super-computers, such as those provided by the NSF’s XSEDE program. The reality is however more complex: while massively-parallel architectures are indeed ideally suited to carry out tasks where many independent computations can be executed in parallel (e.g., like computing the forces acting on a large number of atoms), they provide only limited benefits when one needs to execute a large number of interdependent tasks. For example, advancing the positions of atoms from time t to time t+dt requires first completing the task that advances the positions from time t-dt to t, so these two tasks cannot be executed in simultaneously. Large computers are therefore ideally suited to simulate large systems for short times, but cannot extend the simulation time of small systems. This has led to a dramatic asymmetry in our ability to leverage today’s largest computers to extend simulation length- and time-scales.
Physicists and chemists have been developing methods to overcome this limitation for many years. For example, the Parallel Replica Dynamics (ParRep) method, introduced about 20 years ago by Arthur Voter at Los Alamos National Laboratory, introduces a strategy to parallelize MD over time by using multiple replicas of the system of interest, thereby greatly extending the timescales amenable to direct MD simulation. This is possible so long as one foregoes the generation of a trajectory that is continuous in phase space in favor of a discretized trajectory that represents the evolution of the system as it passes through discrete states. Voter initially showed that such a discretized state-to-state trajectory can be exactly generated in parallel so long as the state-to-state dynamics is Markovian, which is the natural limit when state-to-state transition become increasingly rare. While this yielded an extremely powerful method, its behavior away from the ideal Markovian limit remained poorly understood.
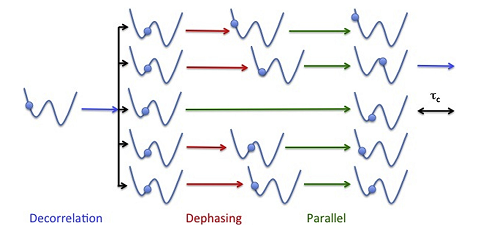
- Illustration of the ParRep algorithm. An initial configuration is replicated over all available processors. The momenta on the new replicas are randomized and the dynamics propagated forward until the system has remained in the initial well for at least a time tc (dephasing stage). All replicas are then evolved independently until the first one observes a transition (parallel stage), at which point all replicas are halted. The replica where the transition occurred then evolves until it spends a time tc in the same well (decorrelation stage). At this point, the simulation times accumulated by all replicas during the parallel and decorrelation stages are added to the simulation clock, and the cycle is repeated. This allow simulation time to be accumulated in parallel, allowing for significant extension of the simulation timescales. By leveraging the concept of quasi-stationary distribution, a collaboration between applied mathematicians and domain scientists has demonstrated that the accuracy of trajectories generated by ParRep increases exponentially with tc, thereby preserving the exceptional predictive power of MD. Reproduced from Perez et al., Computational Materials Science 100, 90 (2015)
Beginning at an IPAM workshop in 2012, a group of applied mathematicians became intrigued by the simplicity and elegance of the method, but were unsettled by the lack of understanding of the errors present in typical, non-ideal, scenarios. Over the next six years, the active community of mathematicians and domain scientists that developed following this initial impulse met again for a series of additional workshops at IPAM. The researchers came to develop an extremely powerful framework to better understand rare event dynamics in general, and ParRep in particular. This new framework centers upon the concept of the quasi-stationary distribution (QSD), the limiting distribution established by a dynamical system conditional on not escaping a given region of configuration space. The QSD possessed the unique property that, once established, the statistics of following escapes from the specified region of space is exactly Markovian. The team established that the key factor controlling the accuracy and efficiency of ParRep is not whether or not the state-to-state dynamics is originally Markovian, but instead the rate at which the QSD is established. This insight proved extremely powerful because it offered a way to systematically trade computational efficiency for improved accuracy, no matter how states are defined.
These fundamental insights led to a wealth of new developments that were finalized or presented at the IPAM program on “Complex High-Dimensional Energy Landscapes”, including applications to bio-molecules, and the introduction of prediction and speculation in the so-called “Parallel Trajectory Splicing” (ParSplice) method. ParSplice was recently chosen as one of the methods supported by the Department of Energy in order to efficiently leverage upcoming exascale architectures. The quasi stationary distribution approach was also useful from a theoretical viewpoint, to draw rigorous connections between different models of the dynamics of molecular systems (Langevin dynamics and Kinetic Monte Carlo). Such rapid development would not have been possible without avenues such as IPAM, where mathematicians and scientists can interact closely and forge new collaborations.
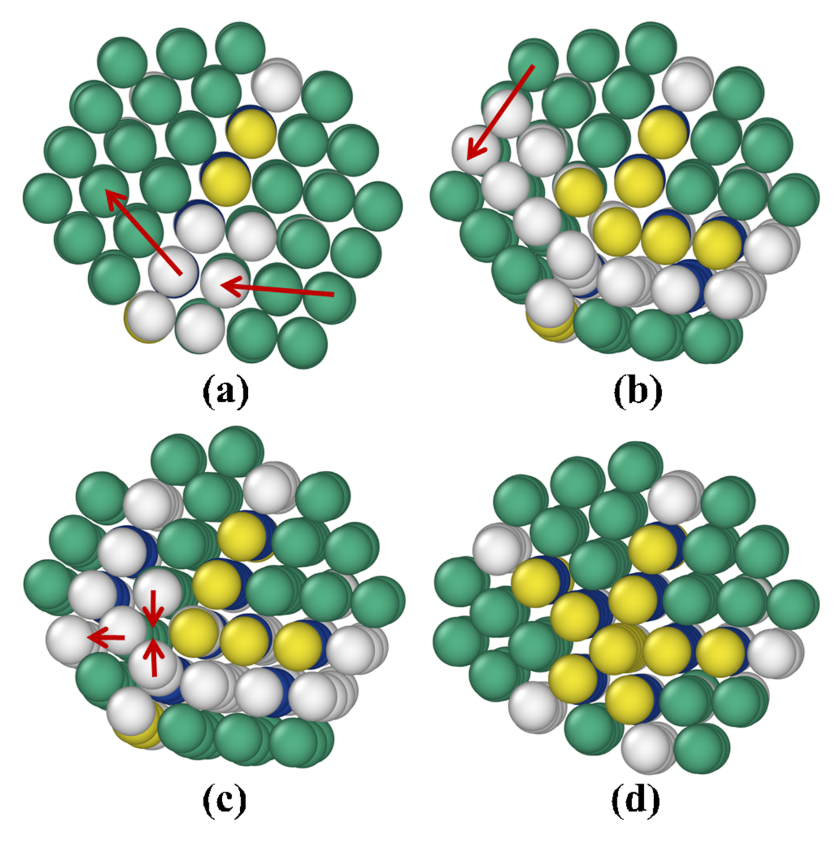
- Process leading to the formation of a five-fold twinned structure in a Platinum nanocluster, as identified by a long simulation using ParSplice, a successor of the ParRep method. Starting from the initial twinned structure shown in panel (a), a concerted slip process leads to the formation of a second twin (panel (b)). A concerted slip of the left-most layer of the cluster then follows, leading up to the configuration shown in panel (c). The last step is the expulsion of an atomic column from the intersection of the two twins. The extension of timescales afforded by methods such as ParRep and ParSplice allows for the direct observation of complex processes that affect the structure and properties of materials. Reproduced from Huang et al., Journal of Computational Physics 147, 152717 (2017).
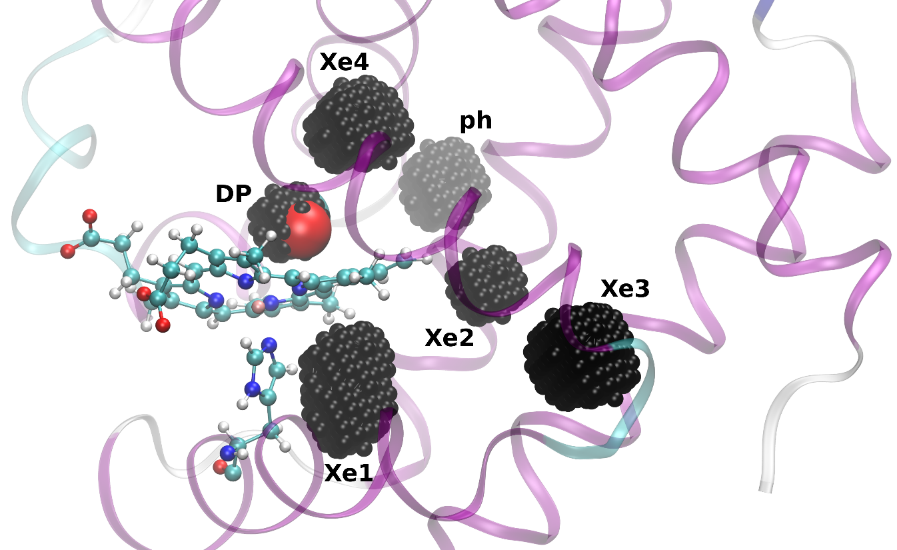
- An example of application of Accelerated Dynamics methods to biological system, to study small ligand migration within the internal network of myoglobin. Typical transition times between cavities range from 1 to 100 nanoseconds. Here, a carbon monoxyde molecule is in the DP cavity, and other cavities are represented.