The economic value to the oil industry of 3D seismic imaging is approximately $11 billion annually. How accurately seismic imaging can be done depends on both the quality of the sensing equipment, but also very much on the effectiveness of the mathematical algorithms that are used. Hence it is an important event when seismic imaging algorithms are improved.

Data: 80% missing traces

Reconstructed Image

In 2004, the Institute for Pure and Applied Mathematics held a 3-month program on  Multiscale Geometry and Analysis in High Dimensions. This program assembled a diverse group of participants, including Emmanuel Candes (Mathematics), David Donoho (Statistics), Terry Tao (Mathematics), Michael Elad (Computer Science), Jean-Luc Starck (Astrophysics), Justin Romberg (Mathematics) and Felix Herrmann (Geosciences) and Herrmann’s graduate student Peyman Moghaddan. During the program, important mathematical progress was made by a group led by Candes and Tao that enabled new nonlinear techniques in stable data recovery from incomplete data.

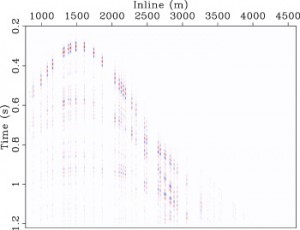
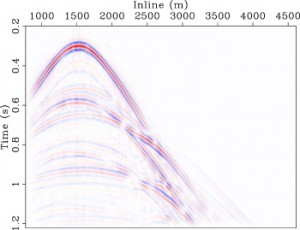
A major problem in seismic imaging is recovery from incomplete data. Felix Herrmann of the University of British Columbia together with collaborators including graduate student Gilles Hennenfent pioneered several new seismic imaging techniques inspired by this mathematical breakthrough. The mathematics is quite sophisticated, capitalizing on the compression of seismic imaging data in the curvelet domain, but the resulting algorithms are highly practical. Indeed, the technique works when as many as 85% of the traces are missing. An interdisciplinary team headed by Herrmann (Geosciences), Michael Friedlander (Computer Science) and Ozgur Yilmaz (Mathematics) is now engaged in developing and implementing these techniques on a project “Dynamic Nonlinear Optimization for Imaging in Seismic Exploration.” DNOISE, together with a related project SINBAD of Herrmann’s group, has received $1.65 million in funding in a dollar for dollar NSERC-private industry collaborative research and development matching grant.